여러분들 안녕하세요! 우기부기 입니다!
이번 시간에는 미분적분학 1장. 집합과 함수 파트에서 수열에 대한 내용을 공부해보려고 합니다! 블로그에 제가 공부한 내용을 포스트하는데 있어서 슬슬 글을 빨리 빨리 올리는 것에 무리가 있다고 생각이 들기 시작했어요.
한 단원을 공부하는데에 있어 적어도 포스팅을 하려면 정확하게는 알고 있어야한다고 생각하고 있어서 공부를 아무리 해도 조금만 더 살펴보고 싶은 느낌이 들거든요...
그런 이유로 글이 빠른 속도로 올라오지는 않겠지만 나중에 많은 글들을 썻을 때, 저와 또한 저와 같이 공부의 뜻을 함께하는 분들의 기본적인 개념서가 될 수 있기를 바라면서 오늘의 글 목차를 쓰도록 할게요!
- 수열의 정의
- 수열의 종류
- 수열의 극한
- 수열의 정의
수열 : 일정한 규칙에 따라 한 줄로 배열된 수의 열,

라고 표기했을 때, 수열 f는

라고 표현할 수 있다.
f에서 표현되고 있는 a들을

이라고 칭하며 이것들을 일반항이라고 칭한다.
- 수열의 종류
등차수열
수열들의 규칙이 일정하게 어떠한 수를 더하거나 빼는 규칙이 있는 수열
일반항 :

등비수열
수열들의 규칙이 일정하게 어떠한 수를 곱하거나 나누는 규칙이 있는 수열
일반항 :

- 수열의 극한
수렴한다
수열

에서 n이 무한하게 커지면 고정된 어떠한 유한한 수 a에 한 없이 가까이 가는 현상이다.
위 내용을 기호로 표현하면,

위 그림처럼 쓸 수 있다.
극한
위 기호에서 a를 an의 극한이라고 한다.
발산
수렴하지 않은 수열을 발산한다라고 칭한다.
유계
모든 자연수 n에 대해서

가 성립할 때 유계라고 한다.
정리 1.1 단조 수렴 정리
위로 유계인 증가 수열은 수렴한다. (상한으로 수렴)
정리 1.2 수열의 극한정리
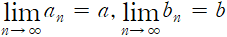
일때,
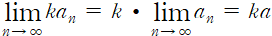
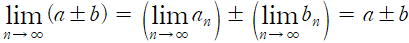
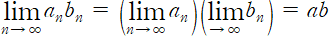
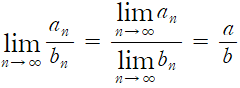
와 같은 형태들은 위와 같이 적용된다.
오늘은 자연스럽게 수열과 수열의 극한에 대해서 알아보았어요 위 단원과 관련된 문제를 풀어서 여러분들에게 최대한 실용적으로 정보를 전달해드리고 싶은데 아직까지는 제가 많이 서툴러서 힘든 것 같네요...
여러분들에게 더 좋은 지식들을 전달할 수 있도록 더 열심히 포스팅할게요! 다들 화이팅! 다음시간에는 '함수의 극한'에 대해서 알아볼까 합니다. 다들 그날까지 공부들 화이팅 하세요!
'우기의 자기개발 > 기초공학수학' 카테고리의 다른 글
| [미분적분학] 1장. 집합과 함수 - 함수 (0) | 2020.08.24 |
|---|---|
| [미분적분학] 1장. 집합과 함수 - 실수의 성질 (0) | 2020.08.23 |
| [미분적분학] 1장. 집합과 함수 - 집합 정리 (0) | 2020.08.22 |


